This article on extrapolation in construction litigation was originally written & published years ago by Ted Bumgardner. The last republishing of the article was at the 2014 West Coast Casualty Construction Defect Seminar.
Statistical Analysis and the science of predicting the whole based on a sampling of the parts is all around us in everyday life. You can’t turn on the TV or pick up a newspaper without seeing the latest approval rating of the President or finding out how many of us are unemployed, filing bankruptcy, getting divorced or like Coke better than Pepsi. We know that these reports are based on sampling; we have come to accept these numbers and have become comfortable with the concept of counting a few to represent many.
Maybe this is why there has been an acceptance in the construction industry of sampling techniques that, when analyzed, are found to be a total misapplication of the basic fundamentals of statistical analysis. Two of the most egregious breaches of good science are in the related areas of:
- Extrapolation of quantities in defect litigation
- The sampling of units in third-party quality assurance inspections
Ironically, in the first case, bad science is being used to get more money out of the insurance companies that underwrite the liability coverage for contractors and developers. In the second case, bad science is being used to create a false level of comfort for those same carriers hoping to stop the bleeding caused by the defect litigation.
Statistics 101 in Construction Defect Litigation
The science of inferential statistics is derived from the Central Limit Theorem, first discovered in the early 19th century. It is the mathematical centerpiece of the ability to generalize to the population from which the sample is drawn. The mathematical corollary of the Central Limit Theorem is known as “The Law of Large Numbers.” The mathematics derived from these fundamentals allows us to forecast with calculable levels of certainty that a population value is within a specific range of values.
Three basic requirements to making this all work are:
- The sample must be randomly selected
- The sample must be of adequate size
- The population must be defined.
Properly applied, this science can be used to sample from a universe of anything from people to plants to construction projects. If improperly applied, the results are no more than a guess.
Defects litigation is a very expensive process. Plaintiff experts are asked to identify defects and opine on the extent of defects that are not apparent in a visual inspection. The cost, for example, to open up a wall, spray test a window, and check it for leaks can cost over $2,500 per window. Plaintiff attorneys, therefore, want to limit the up-front expense of extensive invasive testing. The experts have developed the practice of investigating a few and extrapolate their findings to the total litigated population.
In one recent case, a well-known plaintiff expert tested 12 windows and found leaks at six (6). He then extrapolated that 50 percent of the windows were defective, or 4,350 out of a total population of 8,700 windows. His repair recommendation called for the removal and replacement of windows at a cost of over $4.8 million. The window issue was one of over 100 alleged defects, the majority of which were “extrapolated” in a similar fashion.
His extrapolation, which is typical in the defects industry, overlooked all three of the basic requirements precedent to a valid statistical projection.
Random Sampling
At his deposition, the plaintiff expert stated that he “took a map of the project and picked a couple here and a couple there to make a list of homes,” then the plaintiff attorney arranged access with homeowners willing to allow the invasive testing from the list.
This was by definition not a random sample. A truly random sample would have been arrived at by numbering each window then using a random number generator like that in an Excel spreadsheet program to pick the windows to be tested, then those specific windows would have been tested to form the basis of an extrapolation. Many statistical references state that there is no mathematical basis for the substitution of a single unit because any non-response can lead to bias.
According to Dr. John R. Weeks, Ph.D., a professor of geography and renowned demographer at San Diego State University:
“If the sample was not selected using scientifically valid random procedures, it is not mathematically defensible to generalize the findings beyond the units that were inspected.”
Defined Population
Construction is the product of the efforts of many diverse subcontractors and varying crews operating in changing external conditions. Large single family detached projects are built over long periods of time with multiple small phases, multiple subcontractors of the same trade, and many crew changes. The quality of the work of any specific crew cannot be reliably extrapolated to form the basis of analysis of the work of another crew. In the referred case, for example, there were four different stucco subcontractors involved in various phases of the project. The plaintiff expert’s extrapolation failed to distinguish one subcontractor’s work from another
Sample Size
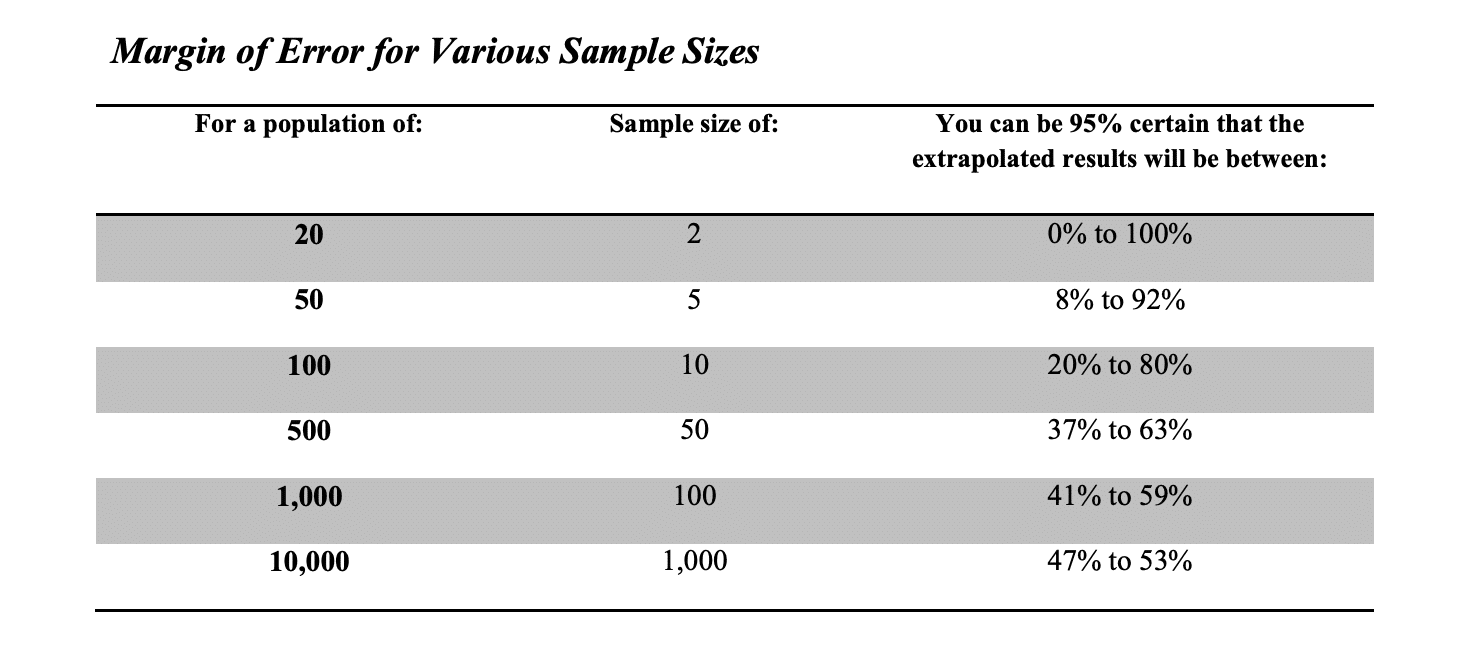
Assuming that the sampling was random, which it was clearly not, and that the sampling was of a defined population, which it was also not, we can easily determine the adequacy of the sample size using any readily available sample size calculators from the Internet. Using the numbers from this case, for example, the plaintiff expert can be 95 percent certain that his results were within a confidence interval (margin of error) of +/- 28 percent, or something between 22 percent and 78 percent. Therefore, based on the cost to repair a window he can be 95 percent certain that the alleged defect will cost somewhere between $1.5 million and $5.5 million to repair.
Based on these numbers, it sure looks like the plaintiff expert is using a mighty big dartboard. This type of absurd extrapolation is not the exception, but the rule and is “bought into” by experts on both sides as well as mediators with surprising frequency. It seems that the closest thing to a standard utilized by the “experts” is somewhat of a convention that 10 percent is an appropriate sample size for all population sizes. The following chart shows the confidence interval (margin of error) for various sample sizes and populations assuming a 50 percent failure rate.
When the test results are more consistent, the reliability of extrapolation improves. For example, if two (2) of 20 are tested and both fail, the margin of error for the extrapolation is +/- 13%, but if a third item is tested and it passes, the margin of error for extrapolation jumps to +/- 50% making any extrapolation totally meaningless.
As you can see, extrapolated results become almost meaningless in populations of less than 1,000. I guess that’s why the basis of all statistical analysis, the Central Limit Theorem is known as the “Law of Big Numbers”. In residential construction installation issues, we are typically working in small numbers when you consider the phase changes, contractor changes, and crew changes that we typically see. We tend to see the big numbers that will tend to work for statistical analysis and extrapolation only in manufactured items and product failures where the populations tend to be over 1,000.
The insurance carriers, after having paid out big money in defects lawsuits, have responded to the risks inherent in underwriting construction liability by requiring that approved 3rd party quality assurance inspectors inspect the work as it goes in place. Qualified 3rd party inspectors can certainly make a significant impact on the quality of work and reduce the risk of defective construction, at least for the work that they actually see as it is going in place. The irony here is that most of the insurance carriers that underwrite single family residential construction only require that 25 percent of the units be inspected. Here again, there is a clear misconception by most insurers and most 3rd party quality assurance firms that 25 percent of a small number of anything has any relevance to the rest of the population. The standard single family detached construction phase is 10 to 12 units. If three (3) of 12 units are inspected, results at the nine (9) other units can be extrapolated to a margin of error of +/- 50%, a statistically meaningless result.
When it comes to inspecting construction, whether for defects investigations or for quality assurance in new construction, we need to leave the statistical extrapolation out of the equation and rely only on what we can actually see. It is certainly cheaper to only look at a few and convince ourselves that we think we know something about the others that we haven’t seen, but with the relatively small numbers encountered on construction projects and all of the variables encountered in the construction process, we need to insist on relying only upon what we can see. Defects experts should focus on identifying the real problems with a project and what has failed should be repaired. Quality assurance inspections should be based on visual observation of all the units so there will be fewer defects cases for us to argue over these absurd extrapolations.
To learn more about VERTEX’s Construction Claims Consulting services or to speak with a Construction Expert, call 888.298.5162 or submit an inquiry.
Author: Ted Bumgardner
This article was originally published by Xpera Group which is now part of The Vertex Companies, LLC.



